Using unthresholded effect size maps
We often face the situation where a particular effect in our imaging data does not survive strict familywise error control, but for various reasons does seem plausible enough to report. In this situation, and indeed in general, one attractive option is to report the entire effect size map of your analysis.
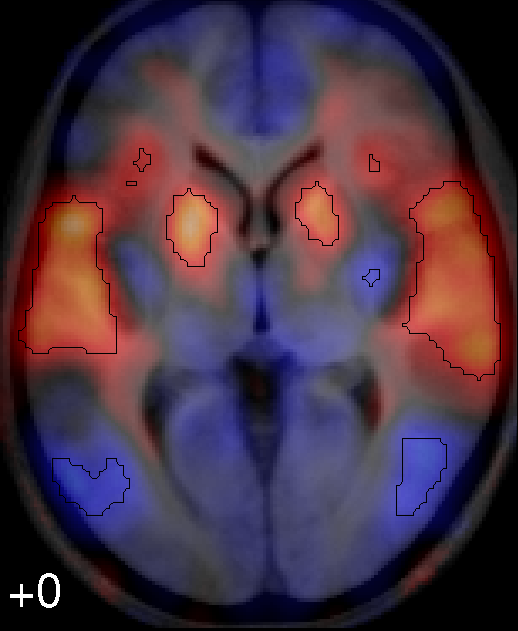
If you want to be able to report the areas that were significant at corrected thresholds also, this is easy to do with a combined map like this one:
 .
.
(I used DisplaySlices with a continuous flot.lut colormap for the activation image, and overlaid contours from the SPM thresholded at FWE p<0.05).
The argument for unthresholded maps is twofold: unthresholded maps give better data with which to localize function, and are more useful for meta-analysis.
Unthresholded maps are useful for localizing function
The thresholded maps we are all used to can be seriously misleading for localizing function:
Jernigan TL, Gamst AC, Fennema-Notestine C, Ostergaard AL. More "mapping" in brain mapping: statistical comparison of effects. Hum Brain Mapp. 2003 Jun;19(2):90-5
The argument in this paper is very simple.
Let's say you only present a thresholded SPM map for task X, and you only found area A activated above threshold. You then say: area A is involved in task X. However, as we all know, just because something isn't significant, doesn't mean it isn't there. So, the fact that A is significant, and the rest of the brain isn't, is perfectly compatible with the whole brain being actually activated, and A being just above threshold due to noise. So, when we say A is activated by X, we are really saying, maybe the whole brain is activated by X, and A got above threshold. We can't even say A is particularly activated by X, unless we test the level of activation in A directly against the rest of the brain. So, A is activated by X, on its own, has very little value for localizing function. Therefore, the classic thresholded SPM has very little value for localizing function.
So, in order to localize function, you need some estimate of what is, and what is not activated. To do this in a direct way, you would have to compare activation in brain areas directly, and this is difficult, and extremely rare. The continuous map on its own does not provide you with such a test, but at least it allows you a preliminary comparison, and makes the problem much clearer.
Comparison with behavioural experiments
Let us say you are doing a study on patients with dorsolateral prefrontal cortex damage and test them on (task A) spatial working memory and (task B) a Stroop task. A gives p=0.05, B gives p=0.06. You don't report the result for B at all and only report A, and say, 'frontal lobe patients are impaired on spatial working memory'. It would be true to say this, but it would be very misleading, because it implies that patients with frontal lobe lesions are particularly impaired on spatial working memory, for which you have no good evidence. The reason that 'frontal lobe patients are impaired on spatial working memory' implies the unsupported 'frontal lobe patients are particularly impaired on spatial working memory' is that, if frontal lobe patients are impaired on all tests, or even all tests of memory, stating that they are impaired on spatial working memory is entirely uninteresting.
Obviously I'm drawing a parallel with the thresholded SPM map. Again we have done many measurements. Again we are simply not reporting the results of the large majority of the measurements. Let's say 'Area X is activated by task A'. On its own, this is misleading, because this statement would be entirely uninteresting if it is also true that the whole of the rest of the brain is activated to a similar extent. So, I believe that 'Area X is activated by task A' actually strongly implies 'Area X in particular is activated by task A' for which it is very rare to present any good evidence.
The unthresholded map is more useful for meta-analysis
This is quoting from an SPM email by Tom Nichols:
- Here's my $0.02 on the issue of looking at unthresholded maps. If you were to ask a random statistician if their data analysis strategies included completely screening-out and ignoring the results of all non-significant tests, I think you'd find few if any would say "yes". I think it's safe to say that no statistician would recommend blinding yourself to all results except those corresponding to "Reject Ho". For example, basic statistics courses cover the issue of practical significance vs. statistical significance, stressing that one must look at results in real-world units. In the context of fMRI, here are two extremes that illustrate the importance of practical vs. statistical significance. If one obtains a very significant result but it corresponds to a 0.01% BOLD change, it should be clearly reported as such, so that readers know you are reporting an incredibly subtle effect. On the other hand, if a 100% BOLD change was found that was non-significant, we'd like to know what gave rise to such a result; most likely there is huge variance, but huge variance tells you that there was virtually no power to detect a result even if Ho was false!. (And this then ties in to the need for looking at standard deviation images, if only to identify regions with high risk of Type II errors.)
Unthresholded maps for assessing data quality
In my experience, continuous maps give a much clearer picture of the quality of the data.
