Computing the Noise Covariance Matrix
The noise covariance matrix is needed for the computation of the inverse operator.
Ingredients for this script are
* raw MEG data files (e.g. those used for averaging, after maxfilter)
* a description file (see below)
You can visualise the covariance matrices in Matlab.
The end result is a fiff-file containing the noise covariance matrix, which can be read into Matlab using mne_read_noise_cov.
Note: For some applications, for example single-trial analysis, you should use a covariance matrix computed on empty-room data. Pre-processing for these data should be as similar as possible to the raw data files used for analysis.
The parameters below are reasonable choices for standard analyses. However, these Wiki pages are not supposed to substitute the MNE manual, reading papers, and discussions with more experienced researchers.
#
## Your variables:
datapath='<myrawMEGdatapath>' # root directory for your MEG data
# MEG IDs (your directory structure may differ)
subj_pre=(\
'meg10_0001' \
'meg10_0002' \
'meg10_0003' \
)
# MEG subdirectories (your directory structure may differ)
subj_dir=(\
'100001' \
'100002' \
'100003' \
)
## Processing:
nsubjects=${#subj_pre[*]}
lastsubj=`expr $nsubjects - 1`
for m in `seq 0 ${lastsubj}`
do
echo " "
echo " Computing covariance matrix for SUBJECT ${subj_pre[m]}"
echo " "
mne_process_raw \
--raw ${datapath}/${subj_pre[m]}/${subj_dir[m]}/rawMEGfile_raw1.fif \
--raw ${datapath}/${subj_pre[m]}/${subj_dir[m]}/rawMEGfile_raw2.fif \
--raw ${datapath}/${subj_pre[m]}/${subj_dir[m]}/rawMEGfile_raw3.fif \
--eventsout ${datapath}/${subj_pre[m]}/${subj_dir[m]}/rawMEGfile_raw1-eve.txt \
--eventsout ${datapath}/${subj_pre[m]}/${subj_dir[m]}/rawMEGfile_raw2-eve.txt \
--eventsout ${datapath}/${subj_pre[m]}/${subj_dir[m]}/rawMEGfile_raw3-eve.txt \
--projon \
--cov cov_desc1.cov \
--cov cov_desc2.cov \
--cov cov_desc3.cov \
--savecovtag -cov \
--gcov ${datapath}/${subj_pre[m]}/${subj_dir[m]}/covmat-cov.fif
done # subjects
Covariance Matrix Description File
where the covariance description files cov_desc?.cov are of the form
cov {
gradReject 200e-12 # artefact rejection thresholds
magReject 3e-12
eegReject 120e-6
eogReject 150e-6
logfile YourLogFileName.txt # logfile that will contain some useful information
fixSkew # Fixes problems with trigger onsets on different bits
def {
event 1 # trigger code
tmin -0.2 # interval used for covariance computation
tmax 0
basemin -0.2 # interval used for baseline correction
basemax 0.0
}
def {
event 2
tmin -0.2
tmax 0
basemin -0.2
basemax 0.0
}
def {
event 3
tmin -0.2
tmax 0
basemin -0.2
basemax 0.0
}
}If the parameters are the same for all input files, you only have to specify one description file. For more details and options see the MNE manual.
Visualise Covariance Matrices
The following script allows you to visualise covariance matrices for EEG (if used), magnetometers and gradiometers separately:
% Will read MNE covariance matrix files (*.fif)
% and visualised them separately for magnetometers, gradiometers and EEG
% EEG will be average-referenced
% Olaf Hauk, Nov 2010
covpath = '/YourPathToData/'; % root directory for data
covname = 'YourFilename.fif'; % filename for MNE covariance matrix files in subject directories
% Specify subject information: MEG ID 1, MEG ID2 (may depend on your experiment)
% the script will look for covpath/subject{x}{1}/subject{x}{2}/covname as covariance matrix
cnt = 1;
subject{cnt} = {'meg10_0005', '123456'};
cnt = cnt+1;
subject{cnt} = {'meg10_0006', '654321'};
cnt = cnt+1;
subject{cnt} = {'meg10_0007', '162534'};
cnt = cnt+1;
nr_subs = length(subject); % number of subjects specified
for ss = 1:nr_subs, % for all subjects...
filein = fullfile( covpath, subject{ss}{1}, subject{ss}{2}, covname ); % input filename of covariance matrix file
fprintf(1, '\nReading covariance matrix from %s\n', filein);
covmat = mne_read_noise_cov( filein ) % read noise covariance matrix using MNE Matlab tool
channames = covmat.names; % names of channels
indices_EEG = strmatch('EEG', channames); % indices for EEG channels
indices_MEG = strmatch('MEG', channames); % indices for MEG channels (grads+mags)
for i=1:length(indices_MEG),
lastnum(i) = str2num( channames{indices_MEG(i)}(end) ); % get last number of MEG channel names
end; % i
indices_mags = indices_MEG( find ( lastnum == 1 ) ); % find magnetometer indices
indices_grads = indices_MEG( find ( (lastnum==2)+(lastnum==3) ) ); % find gradiometer indices
fprintf(1, 'There are %d magnetometers and %d gradiometers.\n', length(indices_mags), length(indices_grads));
figure; % create new figure
if ~isempty(indices_EEG), % if file contains EEG...
nr_EEG = length(indices_EEG); % number of electrodes
fprintf(1, '...oh, and %d EEG electrodes.\n Average referencing EEG.\n\n', nr_EEG);
covmatEEG = covmat.data(indices_EEG, indices_EEG); % separate EEG covariance matrix
avgop = eye(nr_EEG) - ones(nr_EEG)/nr_EEG; % average reference operator
covmatEEG = avgop*covmatEEG*avgop; % apply average reference to EEG covariance matrix
nr_plots = 3; % plot mags, grads and EEG
subplot(1,nr_plots,1);
imagesc( covmatEEG );
axis( 'square' );
colorbar;
th = title(['EEG ' subject{ss}{1}]); set(th, 'Interpreter', 'none');
else,
nr_plots = 2;
end; % plot mags and grads (no EEG)
covmatmag = covmat.data(indices_mags, indices_mags); % separate mags covariance matrix
subplot(1,nr_plots,2);
imagesc( covmatmag );
axis( 'square' );
colorbar;
th = title(['Mags ' subject{ss}{1}]); set(th, 'Interpreter', 'none');
covmatgrad = covmat.data(indices_grads, indices_grads); % separate grads covariance matrix
subplot(1,nr_plots,3);
imagesc( covmatgrad );
axis( 'square' );
colorbar;
th = title(['Grads ' subject{ss}{1}]); set(th, 'Interpreter', 'none');
end; % ssThe result may look something like this:
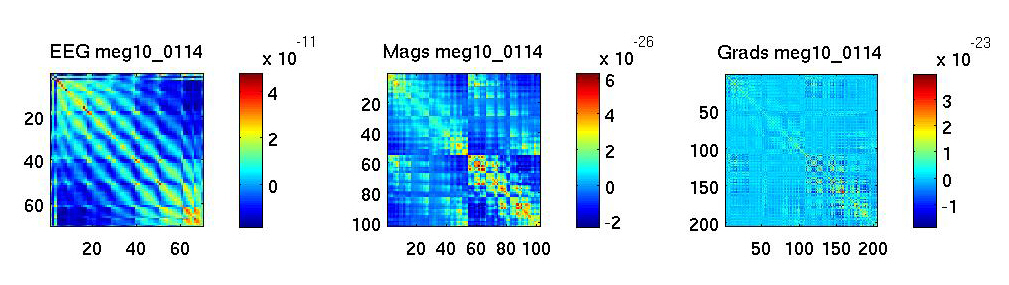
Note: The patterns in these images are due to the spatial arrangements of electrodes and sensors. They may therefore vary for different sensor configurations. The main thing to look out for are channels with huge covariances, or flat channels, or patterns that suggest that all electrodes measured the same signal (indicating a problem with the reference etc.). The EEG in this example was average-referenced, and the MEG data maxfiltered.
